Best-Mogelijke GIS-Oplossingen

Blog

Inzicht in de ontvangstplicht

Waterschap Brabantse Delta heeft aan Gunneman GIS & Geomatics gevraagd een GIS analyse te maken die aangeeft wie verantwoordelijk is voor het vrijkomend maaisel bij maaiwerkzaamheden aan sloten en bermen. Binnen het beheergebied van de Brabantse Delta is een gezamenlijk project gestart om efficiënter het onderhoud aan sloten en bermen uit te voeren. Deze samenwerking is met een aantal inliggende gemeenten en Staatbosbeheer samen met het waterschap gestart.

Wettelijk is het verplicht om het maaisel uit de gemaaide sloten en bermen te “ontvangen” en daarmee af te voeren. Voor de deelnemers is het hierdoor noodzakelijk te weten wie vrijkomend maaisel op zijn perceel moet ontvangen. Om inzicht te verkrijgen en daarnaast gelijk een indicatie over het aantal meters land dat ontvangstplicht draagt, oftewel de ontvangstplichtlengte, zijn berekeningen nodig. Handmatig meten is een hele grote opgave waardoor geautomatiseerd een stuk goedkoper is. Aan de basis van deze berekeningen staan de perceelvlakken van de gemeenten en de te onderhouden waterganglijnen als databronnen ten grondslag.

De resultaten van deze berekeningen kunnen vervolgens gebruikt worden voor aanbestedingen. Tenslotte kan er aan de ontvangstplichtlengte de hoeveelheid werk afgeleid worden en is het daarmee een indicator hoeveel het afvoeren gaat kosten. Het berekenen van de ontvangstplicht draagt dan ook bij aan een data-gedreven wijze van werken.

Het Verschil tussen Modellen en de Weerbarstige Praktijk

“Zo gezegd, zo gedaan!”. Het lijkt een zogeheten “eitje” om deze klus te klaren. Bedenk dat aan de weerszijden van de waterganglijnen een perceel ligt en je bent al bijna klaar, zou je zeggen. Het hoeft enkel nog technisch uitgevoerd te worden in een GIS-pakket om de juiste relaties tussen de percelen en de waterganglijnen te vinden.

Een gemiddeld GIS Specialist draait er zijn/haar hand niet voor om en voert de volgende stappen uit om:

een buffervlak van de waterganglijn te maken óf de waterganglijn te verplaatsen;
een (gemeentelijk) perceel te selecteren;
een ruimtelijke relatie maken op basis van eventuele overlap met het perceel.

Zie Figuur 1.

Figuur 1:

Hier is het resultaat te zien van het maken van een buffervlak (in het lichtblauw) voor een waterganglijn (getekend in donkerblauw). De percelen zijn hier in het groen aangegeven. In paars is de overlap tussen het buffervlak met de percelen te zien.

Modellen Getoetst in de Praktijk

“En daar begint de ellende dan.” De praktijk is weerbarstiger dan je in eerste instantie zou vermoeden. Tijdens het uitvoeren van data-analyses blijken er talrijke uitzonderingen op het model dat je in je hoofd had te bestaan. Zie voor een voorbeeld het verschil wat er tussen het model in je hoofd en de geodata in de praktijk in Figuur 2 en Figuur 3.

Figuur 2:

Dit is een voorbeeld van een perceptie hoe een watergang en aangrenzende percelen getekend is en waaruit de ontvangstlengte berekend wordt. De percelen zijn hier in het groen weergegeven, terwijl de watergang in het blauw is weergegeven. Over het algemeen zijn percepties van modellen eenvoudiger dan die in de werkelijkheid.

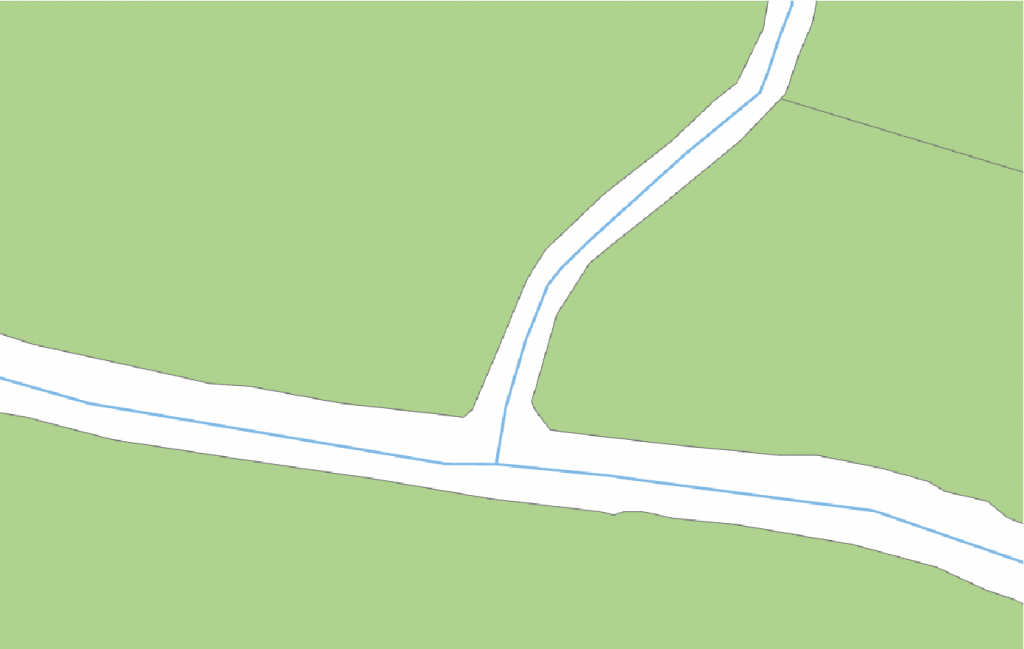
Figuur 3:

Dit is het getekende model van de werkelijkheid. Te zien zijn meerdere watergangen, getekend als blauwe lijnen, en de percelen die als groene vlakken zijn weergegeven. Te zien is dat waterganglijnen bij elkaar komen en dat meerdere percelen langs een watergang liggen. De datawerkelijkheid is hier rigoureus anders dan het model wat “in het hoofd” zit.

Een van de belangrijkste foutenbronnen is dat de afstand van de getekende waterganglijn tot een perceel sterk kan variëren. Er kan daarmee niet gekozen worden om met één afstand alle ruimtelijke relaties (op basis van overlap) tussen de waterganglijnen en de percelen aan te maken. Met één enkele afstand bestaan er vele scenario’s waarbij óf de afstand te kort is gekozen en daarmee geen overlap wordt bewerkstelligd (en daarmee geen ruimtelijke relatie aangemaakt kan worden) óf dat deze lang is en achterliggende percelen geselecteerd worden die geen ontvangstplicht kunnen hebben.

Figuur 4.

Een voorbeeld waarbij voor deze casus de buffergrootte te klein is en niet de perceelgrenzen aan één zijde bereikt. Een relatie met het linkerperceel kan niet gelegd worden, terwijl er wel een relatie gelegd kan worden met het rechterperceel.

Figuur 5:

Een voorbeeld waarbij voor deze casus de buffergrootte te groot is. Hierdoor wordt er een relatie gelegd met een perceel dat achter een ander perceel ligt, terwijl voor dat perceel geen ontvangstplicht geldt.

Daarnaast bestaan er nog veel meer foutenbronnen:

de waterganglijn hoeft niet in het midden te liggen tussen 2 percelen, maar kan aan beide zijden verschillende hellingshoeken hebben waardoor links en rechts de afstanden tussen de linker- en rechterzijde verschillen;
perceelvormen met aanzienlijke inhammen of uitsteeksels waardoor het meten van de ontvangstplicht moeilijk wordt;
percelen die gedeeltelijk achter andere percelen liggen waarmee de grenzen tweemaal of vaker aan de waterkant liggen;
fouten die ontstaan omdat een waterganglijn aan meerdere percelen ligt en daarmee meerdere ruimtelijke relaties aangaat;
fouten die ontstaan omdat meerdere waterganglijnen aan een perceel liggen en daarmee meerdere ruimtelijke relaties aan gaan;
het aanmaken van buffers blijkt dat bij de kop en de staart soms rare vervormingen van de gevormde buffervlakken optreden. Bijv. als een lijnsegment een scherpe hoek heeft bij het begin of einde van een waterganglijn; enz.

Zie Figuur 4 en Figuur 5 waar verschillende afwijkende scenario’s te zien zijn waarin het aanmaken van een ruimtelijke relatie moeilijk is.

Sommige foutenbronnen zijn oplosbaar. Bijvoorbeeld wanneer een waterganglijn meerdere relaties kan aangaan. De zogenaamde “M X N”-relaties tussen waterganglijnen en percelen kunnen met slim programmeerwerk goed opgelost worden.

Anderen zijn moeilijker of niet op te lossen: het is “knap lastig” om de ontvangstplicht te berekenen voor percelen die inhammen of uitsteeksels hebben. Als deze scenario’s niet de overhand hebben, dan kunnen afwijkingen in de berekeningen allicht geaccepteerd worden.

Het is zaak daarbij dat de impact van fouten klein blijft en daarmee dat er tijdens het programmeren business rules snel geïmplementeerd en getest worden. Op deze manier kunnen modellen in de praktijk getest worden en kunnen verwachtingen en kosten gemanaged worden.

Best-mogelijke GIS-oplossingen

Er werd al eerder genoemd dat de grootste foutenbron de variabele afstand tussen de waterganglijnen en de (gemeentelijke) percelen is.

Om tot een goede oplossing te komen voor dit vraagstuk is het van belang om te realiseren dat het vraagstuk anders geformuleerd moet en kan worden. Het is niet de vraag óf een waterganglijn een relatie heeft met een kadastraal perceel. Het is de vraag wat de impact van een relatie tussen een waterganglijn en een kadastraal perceel op de totale berekening heeft op de berekening voor de Aanbesteding.

Door het vraagstuk anders te formuleren kan de impact van fouten genuanceerder bestudeerd worden. Het is acceptabel in de automatische afleiding dat een perceel met een afwijkende vorm onbedoeld alsnog een relatie aangaat met een waterganglijn zolang de impact op de berekeningen klein blijft.

Door het vraagstuk anders te formuleren wordt het mogelijk om gebruik te maken van de best-mogelijke-GIS-oplossingen-methode.

Met best-mogelijke GIS-oplossingen:

worden meerdere kandidaat-oplossingen automatisch gegenereerd. In dit geval bestaan de kandidaat-oplossingen uit verplaatste waterganglijnen op verschillende afstanden.
worden kandidaat-oplossingen gevalideerd aan de hand van een optimalisatiefunctie en wordt er een score berekend;
wordt de kandidaat-oplossing met de beste score geselecteerd als best-mogelijke oplossing.

In de Figuren 6.1 – 6.8 is te zien hoe de best-mogelijke-GIS-oplossingen grafisch tot stand komen. Uiteindelijk komen de scores van alle kandidaat-oplossingen terecht in één tabel

Hier worden alle waterganglijnen verplaatst met 2, 4, 6, 8, 10 en 12 meter.

Vervolgens wordt er geteld hoeveel coördinaten van de waterganglijn overlap hebben met het desbetreffende kadastraal perceel. Daarmee worden de kandidaat-oplossingen gevalideerd.

De kandidaatsoplossing met de meeste coördinaten met overlap met een kadastraal perceel heeft de beste score en wordt geselecteerd als best-mogelijke-GIS-oplossing. Daarmee is de best-mogelijke-GIS-oplossing voor de desbetreffende waterganglijn-perceel-relatie gevonden.

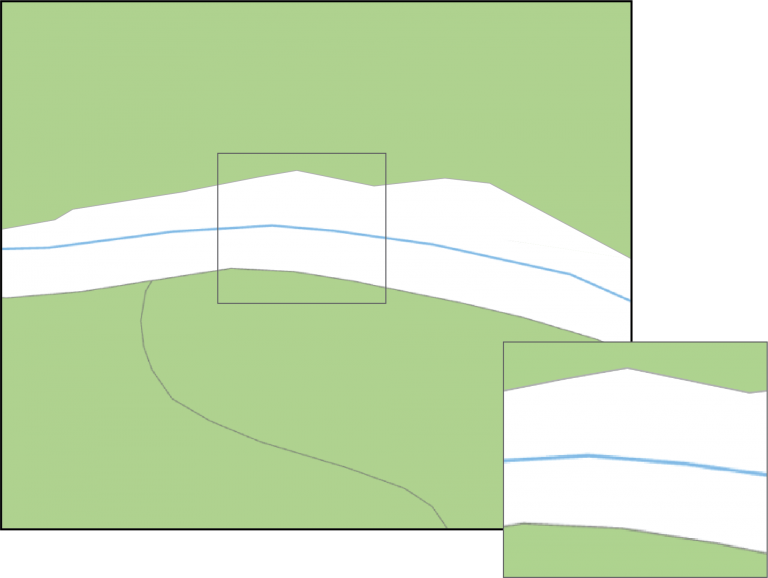
Figuur 6.1:

Dit is de beginsituatie. Te zien is 1 waterganglijn (in het blauw) en 3 percelen in het groen waarover de ontvangstplichtlengte berekend wordt. In de rechterhoek staat een vergroting van de situatie uitgebeeld.

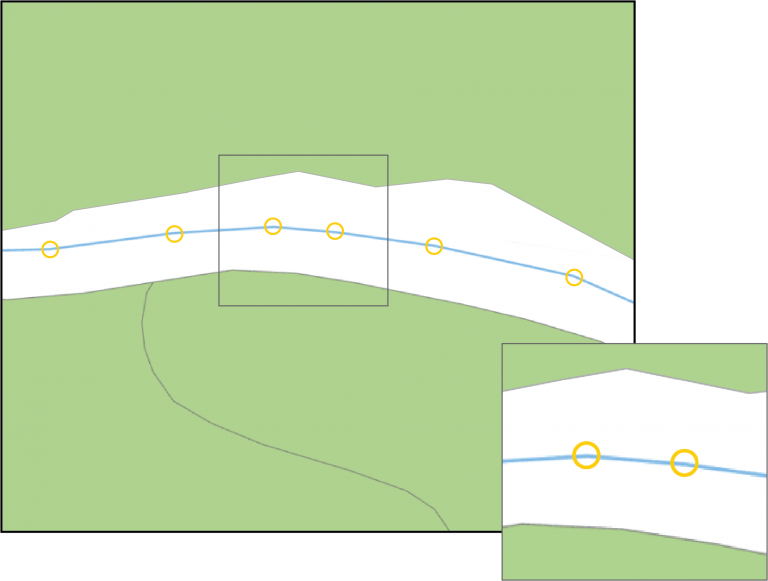
Figuur 6.2:

In gele cirkels worden de punten weergegeven waaruit de waterganglijn is opgebouwd.

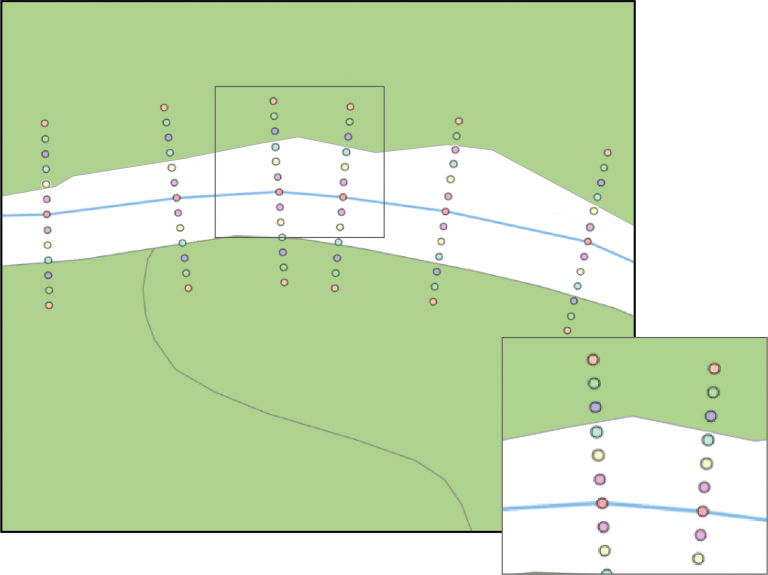
Figuur 6.3:

Langs de waterganglijn worden punten gegenereerd die op een afstand van 2, 4, 6, 8, 10 en 12 meter gezet worden.

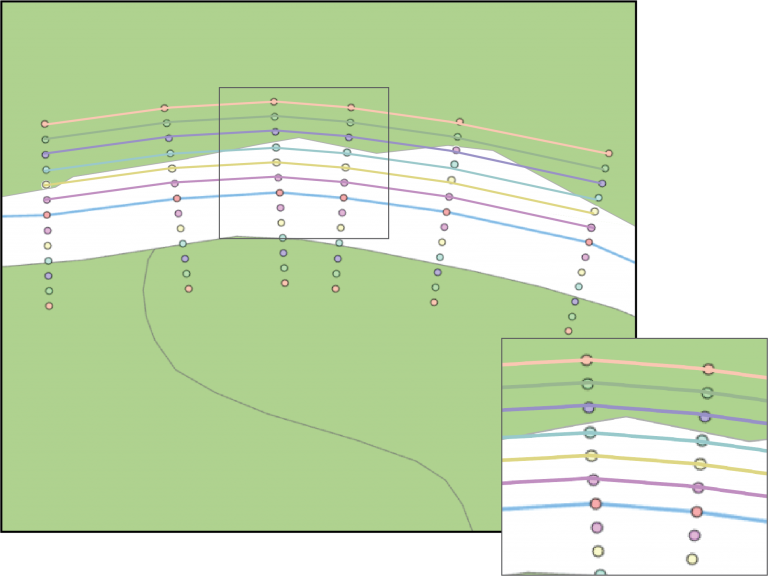
Figuur 6.4:

Alle punten aan een zijde van de waterganglijn op dezelfde afstand vormen een kandidaat-oplossing. Elke kleur stelt hier een andere kandidaat-oplossing voor.

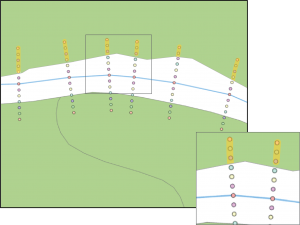
Figuur 6.5:

Voor elk punt wordt nagegaan of deze overlap heeft met een perceel. De punten die hier overlap hebben zijn hier uitgelicht en liggen allen boven de perceelvlakken.

afstand	aantal keren overlap met perceel
0	0
2	0
4	1
6	2
8	5
10	6
12	6

Figuur 6.6:

Er wordt geteld hoeveel punten per kandidaat-oplossing overlap hebben. De kandidaat-oplossing met het grootste aantal overlappende punten is de best-mogelijke oplossing. Hier is er voor gekozen om de kandidaat-oplossing te kiezen die het grootste aantal overlappende punten heeft én die het dichtst bij de waterganglijn ligt. In dit geval is de kandidaat-oplossing op een afstand van 10 meter de best-mogelijke GIS-oplossing.

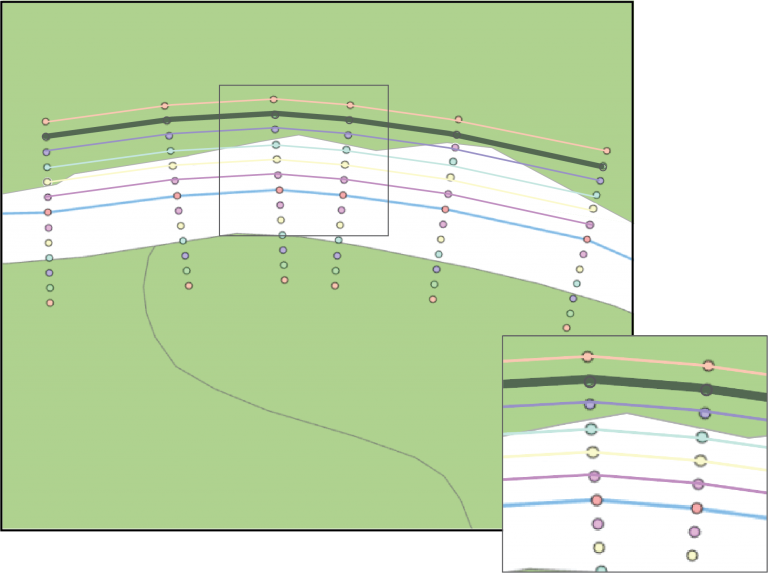
Figuur 6.7:

De best-mogelijke GIS-oplossing wordt geselecteerd en uit de punten wordt een lijn gevormd.

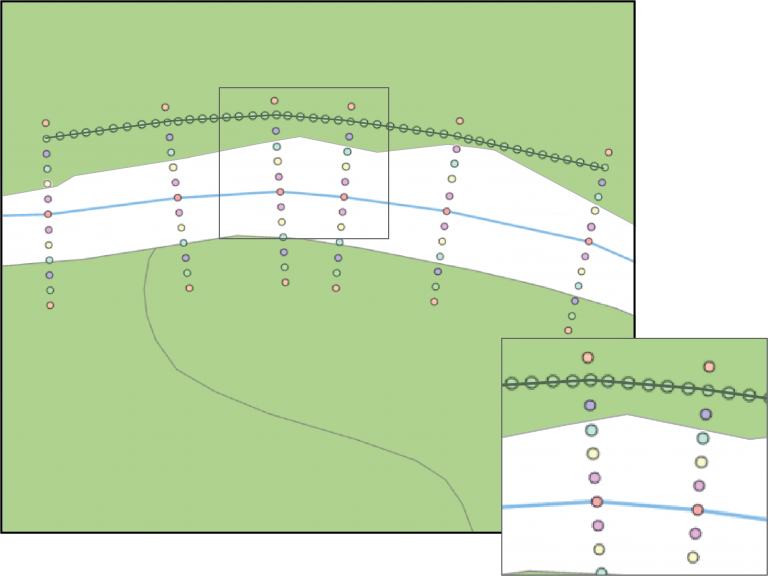
Figuur 6.8:

De lijn wordt verdicht door iedere 1 meter een punt te zetten. Door vervolgens de punten te tellen die overlap hebben met het perceel kan een schatting gemaakt maken van de ontvangstplichtlengte. 87 punten staat gelijk aan (ongeveer) 87 meter ontvangstplichtlengte.

Het Berekenen en Presenteren van de Ontvangstplichtlengte

Na de berekening uitgevoerd te hebben voor alle waterganglijnen is per waterganglijn de ideale afstand tot een perceel bekend. Daarmee is echter nog niet de ontvangstplichtlengte berekend.

Vanwege een (weer) weerbarstige praktijk is er hier gekozen om de verplaatste waterganglijn te verdichten tot 1 punt per meter, en het aantal punten te tellen dat overlap heeft met een perceel. 87 punten die overlap hebben met een perceel komt neer op 87 meter ontvangstplichtlengte voor het desbetreffende perceel.

Het fijne van deze methode is dat niet enkel er een berekening plaatsvindt, maar dat deze ook nog eens presenteerbaar is op een kaart. Met de kaart wordt de berekening voor het aanbestedingsproces transparant en kan eventueel onbegrip of eventuele wrijvingen tussen de Aanbestedende partij en Aannemers beperkt worden.

Best mogelijke GIS-Oplossingen voor Aanbestedingen

Om GIS-oplossingen in te zetten in het faciliteren van berekeningen voor aanbestedingen is het van belang om het vraagstuk te kunnen kwantificeren en de mogelijkheid te hebben om een optimalisatiefunctie op te zetten. Daarnaast zal er rekening gehouden moeten worden dat geografische data tot de categorie “zware data” behoort en daarmee relatief veel rekentijd nodig heeft om tot oplossingen te komen. Het is niet voor niets dat er hier voor “maar” 6 mogelijke afstanden, waar de kandidaat-oplossingen op gebaseerd zijn, gekozen is.

Tegelijkertijd kan het interessant zijn om zoekfuncties naar andere domeinwaarden dan de hier vastgestelde 2, 4, 6 ,8, 10 en 12 meter, te introduceren. Met zoekfuncties hoeft er niet langer meer met vastgestelde waarden gewerkt te worden, maar zoekt de zoekfunctie zelf naar de juiste waarde. Met de introductie van zoekfuncties kan bijvoorbeeld een kandidaat-oplossing gebaseerd op 9,17 meter afstand gevonden worden. Door de domeinwaarden los te kunnen laten kan een hogere precisie van de oplossingen bereikt worden. De keerzijde van de medaille is daarentegen dat het implementeren van een zoekfunctie zorgt voor een grotere complexiteit van de berekening en dat de berekeningen nog zwaarder kunnen worden.

Tenslotte zal er geaccepteerd moeten worden dat er scenario’s bestaan waarbij de best-mogelijke-GIS-oplossing niet voldoet aan de gevraagde berekening. In de automatisering van het berekenen van best-mogelijke-GIS-oplossingen worden impliciet en expliciet aannames gemaakt om tot een wiskundig model te komen. Hierdoor worden niet in alle denkbare scenario’s de beste oplossingen gevonden. Door de impact te bestuderen op de totaalberekening kan vervolgens het wiskundig model verbeterd worden waarmee best-mogelijke oplossingen dichterbij de beste oplossingen komen te staan.

Conclusie

Voor het maken van berekeningen voor aanbestedingen rond beheer van een omgeving is het van groot belang dat de juiste vraag gesteld wordt.

Het is niet de vraag óf er een ruimtelijke relatie gemaakt kan worden tussen ruimtelijke objecten, maar tot in hoeverre de ruimtelijke relatie kwantificeerbaar is en daarmee de kwaliteit van de ruimtelijke relatie te valideren is. Zonder kwalificatie van mogelijke oplossingen is het onbekend wat de impact van fouten zijn.

Het is technisch mogelijk om tot betere best-mogelijke oplossingen te komen door zoekfuncties te implementeren. Het model voor het maken van de berekeningen kan in veel gevallen verbeterd worden als er voldoende ontwikkeltijd en rekentijd beschikbaar is.

Tenslotte dragen best-mogelijke GIS-oplossingen bij in het vinden van betere oplossingen en kunnen, waar mogelijk, ook communicatieve doelen bereiken. Een kaart visualiseert immers de berekeningen. Door verschillende scenario’s te (laten) bekijken wordt er aan vertrouwen gewonnen in het Aanbestedingstraject.